Data Structure Part 2
Graph / Tree / Hash Table
Graph
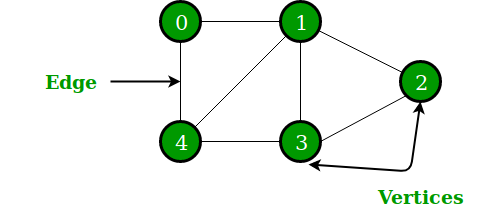
이미지 출처: GeeksforGeeks
- 그래프는 node, node사이를 연결하는 edge로 구성되어있습니다.
- 네트워크 형태의 관계를 저장하기 좋은 데이터 구조로, 복잡하게 얽힌 real life의 정보들을 담아내기 적절합니다.
- edge는 방향 정보를 가질 수 있고, 가중치(weight)도 저장할 수 있습니다. 도로의 길이, 걸리는 시간 등을 가중치로 설정하여 필요한 정보를 충분히 담아낼 수 있습니다.
방향 정보는 SNS에 적용한다면 A유저가 B유저를 follow했다면 단방향. 서로 follow관계면 양방향으로 적용해볼 수 있을 것 같습니다.
자료구조 그래프의 기원은, 객체 간에 짝을 이루는 관계를 모델링 하기 위한 수학적인 이론인 그래프 이론이 1736년에 오일러의 논문에서 처음 제시된 후로 다양한 분야에 사용되다가 컴퓨터 공학에 까지 이르게 된 것이라고 합니다.
그래프 관련 블로그 글 : 트리와의 차이점 정리가 잘 되어있습니다.
Tree

이미지 출처: Eloquent JS
- 트리는 그래프의 하위 개념으로 생각할 수 있습니다.
- 부모-자식 관계가 가능하며, 둘 사이의 edge는 부모에서 자식노드로 향하는 방향성을 갖고 있습니다.
Binary Tree

이미지 출처: wikipedia
- 이진 트리는 자식 노드의 개수를 2개로 제한한 특별한 트리입니다.
이진 탐색 트리는 내용이 정렬되어있어 2진 탐색이 가능한 트리입니다.
완전 이진 트리 포화 이진 트리
이진탐색트리
- 이진 탐색
- 노드 삽입/제거
Hash Table

이미지 출처: CS50 Study
- 데이터의 일부를 hash함수를 이용해 인덱스(숫자)로 만들고, 그 인덱스가 가리키는 공간에 데이터+α를 담는 자료 구조입니다.
- 어떤 데이터를 찾기 위해 테이블 안의 내용을 하나씩 비교할 필요 없이, 검색 키워드를 해시 함수를 통해 인덱스로 변환해, 바로 해당 공간에 담긴 데이터에 접근합니다.
배열을 인덱싱 수단으로 놓고, 값은 엘리먼트(인덱스가 가리키는 공간의 데이터)가 다른 데이터 구조를 참조하도록 해서 사용한다. (인덱스 라는 표현을 사용했지만, 해시 함수에 따라 문자열을 인덱스로서 얻을 수 있습니다. 이 경우 배열이 아닌, linked list 등의 자료 구조에서 그 문자열을 탐색할 키값으로 등록해 인덱싱할 수 있습니다.)
다른 테이블 스트럭쳐에 비해 탐색 속도 면에서 유리합니다. 항목의 수가 많을 때 장점이 더욱 명확해집니다. (항목의 최대 개수를 미리 예측할 수 있는 경우에 효율적이다.)
만약 키-밸류 페어 세트가 고정돼있고 미리 알 수 있으면(삽입삭제불가), 해시 함수, 내용을 담을 테이블 사이즈, 내부 데이터의 데이터 스트럭쳐를 잘 고르면 평균 조회시간을 줄일 수 있습니다. 특히, 충돌없는 해시 함수 혹은 ‘완전 해시 함수’를 고안할 수 있는데 이런 경우에는 키값을 테이블에 저장할 필요가 없습니다.
해시 함수는 입력 데이터에 손실을 발생시킵니다. 다만 같은 입력이라면 손실이 일어나도 같은 결과가 나오므로 재현성이 있어서 의도한 목적에 맞게 사용할 수 있습니다. 이 손실때문에 결과값을 가지고 입력값을 유추하는 것이 불가능해집니다. (제 생각인데 경우에 따라서는 입력값을 특정짓지는 못하고 후보군까지는 만들 수 있을듯 합니다.) 해시의 비가역성에 대한 글